Functional connectivity with nilearn

Functional connectivity with `nilearn`#

In this tutorial, we’ll see how the Python library nilearn allows us to easily perform machine learning analyses with neuroimaging data, specifically functional magnetic resonance imaging (fMRI).

You may notice that the name nilearn is reminiscent of scikit-learn, a popular Python library for machine learning. This is no accident! Nilearn and scikit-learn were created by the same team, and nilearn is designed to bring machine LEARNing to the NeuroImaging (NI) domain.

When performing a machine learning analysis, our data often look something like this:

import pandas as pd

# read_csv can read in just about any plain-text tabular data
data = pd.read_csv('./data/abide2.tsv', sep='\t')
data.head()

	site	subject	age	age_resid	sex	group	fsArea_L_V1_ROI	fsArea_L_MST_ROI	fsArea_L_V6_ROI	fsArea_L_V2_ROI	...	fsCT_R_p47r_ROI	fsCT_R_TGv_ROI	fsCT_R_MBelt_ROI	fsCT_R_LBelt_ROI	fsCT_R_A4_ROI	fsCT_R_STSva_ROI	fsCT_R_TE1m_ROI	fsCT_R_PI_ROI	fsCT_R_a32pr_ROI	fsCT_R_p24_ROI
0	ABIDEII-KKI_1	29293	8.893151	13.642852	2.0	1.0	2750.0	306.0	354.0	2123.0	...	3.362	2.827	2.777	2.526	3.202	3.024	3.354	2.629	2.699	3.179
1	ABIDEII-OHSU_1	28997	12.000000	16.081732	2.0	1.0	2836.0	186.0	354.0	2261.0	...	2.809	3.539	2.944	2.769	3.530	3.079	3.282	2.670	2.746	3.324
2	ABIDEII-GU_1	28845	8.390000	12.866264	1.0	2.0	3394.0	223.0	373.0	2827.0	...	2.435	3.321	2.799	2.388	3.148	3.125	3.116	2.891	2.940	3.232
3	ABIDEII-NYU_1	29210	8.300000	13.698139	1.0	1.0	3382.0	266.0	422.0	2686.0	...	3.349	3.344	2.694	3.030	3.258	2.774	3.383	2.696	3.014	3.264
4	ABIDEII-EMC_1	29894	7.772758	14.772459	2.0	2.0	3080.0	161.0	346.0	2105.0	...	2.428	2.940	2.809	2.607	3.430	2.752	2.645	3.111	3.219	4.128

5 rows × 1446 columns

For our purposes, what’s most interesting is the structure of this data set. That is, the data is structured in a tabular format, with pre-extracted features of interest. This makes it easier to consider issues such as: which features would we like to predict? Or, how should we handle cross-validation?

But if we’re starting with neuroimaging data, how can we create this kind of structured representation?

To understand why neuroimaging data needs some special attention, we will briefly talk about the basics of fMRI.

A brief introduction to functional magnetic resonance imaging#

Functional magnetic resonance imaging (fMRI) is a type of neuroimaging technique that measures brain activity. fMRI data is made up of a series of 3D images (or volumes) of the brain collected at a given frequency. Therefore, a typical fMRI file is a 4D image, with the spatial dimensions (x, y, z) added with the dimension of time t. We could, for example, acquire 1 brain volume every 2 seconds, for 6 minutes, which would result in an fMRI data file consisting of 180 3D brain volumes.

Show code cell source Hide code cell source

import pandas as pd
import numpy as np
from nilearn import datasets
from nilearn import maskers
import matplotlib.pyplot as plt

# change this to the location where you want the data to get downloaded
data_dir = './nilearn_data'

# Let's extract timeseries from one subject in a dataset
haxby_dataset = datasets.fetch_haxby(data_dir=data_dir)
haxby_func_filename = haxby_dataset.func[0]

# initialise a masker
brain_masker = maskers.NiftiMasker(
    smoothing_fwhm=6,
    detrend=True, standardize=True,
    low_pass=0.1, high_pass=0.01, t_r=2,
    memory='nilearn_cache', memory_level=1, verbose=0)

# Apply masker
brain_time_series = brain_masker.fit_transform(haxby_func_filename,
                                               confounds=None)
# Function for visualising 3D voxel
def expand_coordinates(indices):
    x, y, z = indices
    x[1::2, :, :] += 1
    y[:, 1::2, :] += 1
    z[:, :, 1::2] += 1
    return x, y, z

def explode(data):
    shape_arr = np.array(data.shape)
    size = shape_arr[:3]*2 - 1
    exploded = np.zeros(np.concatenate([size, shape_arr[3:]]), dtype=data.dtype)
    exploded[::2, ::2, ::2] = data
    return exploded

# Initialise a figure
fig = plt.figure(figsize=(10,3))

# Visualise the voxel
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax1.set_xlabel("x")
ax1.set_ylabel("y")
ax1.set_zlabel("z")
ax1.grid(False)
colors = np.array([[['#1f77b430']*1]*1]*1)
colors = explode(colors)
filled = explode(np.ones((1, 1, 1)))
x, y, z = expand_coordinates(np.indices(np.array(filled.shape) + 1))

x[1::2, :, :] += 1
y[:, 1::2, :] += 1
z[:, :, 1::2] += 1

ax1.voxels(x, y, z, filled, facecolors=colors, edgecolors='white', shade=False)
plt.title("Voxel (3D)")


# Add timeseries to figure
# random voxel
voxel = 1
ax = fig.add_subplot(1, 2, 2)
ax.plot(brain_time_series[:, voxel])
ax.set_title("Timeseriese of a voxel")

plt.xlabel("Time (s)", fontsize = 10)
plt.ylabel("BOLD signal", fontsize= 10)

from myst_nb import glue
glue("voxel-timeseries-fig", fig, display=False)

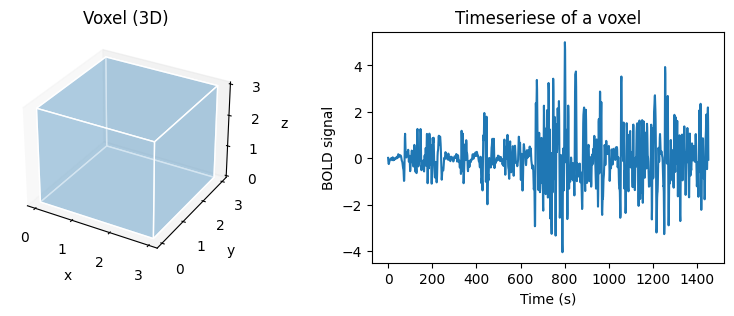
_images/6bc0b3b44a23808748ee0da2a391723c7b156e6d6f7ca491239a5fe6232ef857.png — Fig. 1 Illustration of a volume (voxel), size 3 mm x 3 mm x 3 mm, and the associated fMRI time course.#

A 3D brain volume is formed by several thousand voxels, which are small units of volumes having a coordinate in x, y, z space. In fMRI, for each voxel of the brain, we have several points of measurement of the activity over time, which forms what is called a time series or time course. The time series reflects changes in neuronal activity over time indirectly through the blood delivering energy to activate the neurons, a mechanism called the haemodynamic response. This activity creates a contrast between oxygenated and deoxygenated blood around a population of neurons detectable by the magnetic field, called the blood-oxygen-level-dependent (BOLD) signal.

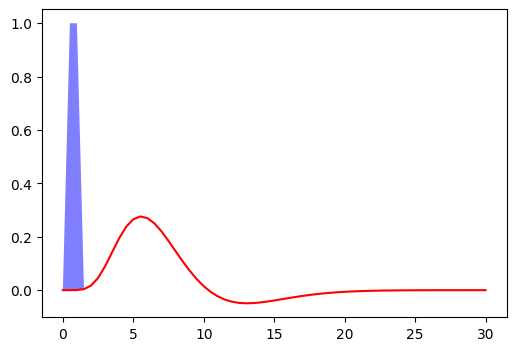
_images/0e14811070b79c027401b84d2112e9c1c56c3dece563ec2a3e5c77d46fc3c861.png — Fig. 2 Hemodynamic response to a unit pulse of one second duration, following the model proposed by [Glo99]. The code generated this figure is adopted from a tutorial in Nilearn, et la. The figure is licenced under CC-BY.#

Neuroimaging data#

Neuroimaging data does not have a tabular structure. Instead, it has both spatial and temporal dependencies between successive data points. That is, knowing where and when something was measured tells you information about the surrounding data points.

We also know that neuroimaging data contains a lot of noise that’s not BOLD signal, such as head motion. Since we don’t think that these other noise sources are related to neuronal firing, we often need to consider how we can make sure that our analyses are not driven by these noise sources.

These are all considerations that most machine learning software libraries are not designed to deal with! Nilearn therefore plays a crucial role in bringing machine learning concepts to the neuroimaging domain.

To get a sense of the problem, the quickest method is to just look at some data. You may have your own data locally that you’d like to work with. Nilearn also provides access to several neuroimaging data sets and atlases (we’ll talk about these a bit later). These datasets are great for developing your analysis workflow and testing new features!

These data sets (and atlases) are only accessible because research groups chose to make their collected data publicly available. We owe them a huge thank you for this! The data set we’ll use today was originally collected by Rebecca Saxe’s group at MIT and hosted on OpenNeuro.

The nilearn team preprocessed the data set with fMRIPrep and downsampled it to a lower resolution, so it’d be easier to work with. We can learn a lot about this data set directly from the Nilearn documentation. For example, we can see that this data set contains over 150 children and adults watching a short Pixar film. Let’s download the first 5 participants.

# change this to the location where you want the data to get downloaded
data_dir = './nilearn_data'
# Now fetch the data
development_dataset = datasets.fetch_development_fmri(n_subjects=5,
                                                      data_dir=data_dir, 
                                                      reduce_confounds = False
                                                     )

Now, this development_dataset object has several attributes which provide access to relevant information. For example, development_dataset.phenotypic provides access to information about the participants, such as whether they were children or adults. We can use development_dataset.func to access the functional MRI (fMRI) data.

Let’s use nilearn.image.load_img to learn a little bit about this data:

from nilearn import image

img = image.load_img(development_dataset.func[0])
img.shape

(50, 59, 50, 168)

This means that there are 168 volumes, each with a 3D structure of (50, 59, 50).

Getting into the data: subsetting and viewing#

Nilearn also provides many methods for plotting this kind of data. For example, we can use nilearn.plotting.view_img to launch at interactive viewer. Because each fMRI run is a 4D time series (three spatial dimensions plus time), we’ll also need to subset the data when we plot it, so that we can look at a single 3D image. Nilearn provides (at least) two ways to do this: with nilearn.image.index_img, which allows us to index a particular frame–or several frames–of a time series, and nilearn.image.mean_img, which allows us to take the mean 3D image over time.

Putting these together, we can interactively view the mean image of the first participant using:

from nilearn import plotting

mean_image = image.mean_img(development_dataset.func[0])
plotting.view_img(mean_image, threshold=None)

Extracting signal from fMRI volumes#

As you can see, this data is decidedly not tabular! What we’d like is to extract and transform meaningful features from this data, and store it in a format that we can easily work with. Importantly, we could work with the full time series directly. But we often want to reduce the dimensionality of our data in a structured way. That is, we may only want to consider signal within certain learned or pre-defined regions of interest (ROIs), while taking into account known sources of noise. To do this, we’ll use nilearn’s Masker objects. What are the masker objects ? First, let’s think about what masking fMRI data is doing:

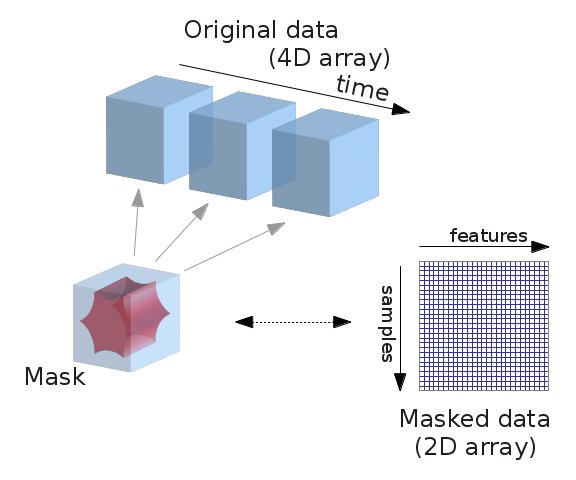
_images/masking.jpg — Fig. 3 Masking fMRI data.#

Essentially, we can imagine overlaying a 3D grid on an image. Then, our mask tells us which cubes or “voxels” (like 3D pixels) to sample from. Since our Nifti images are 4D files, we can’t overlay a single grid – instead, we use a series of 3D grids (one for each volume in the 4D file), so we can get a measurement for each voxel at each timepoint.

Masker objects allow us to apply these masks! To start, we need to define a mask (or masks) that we’d like to apply. This could correspond to one or many regions of interest. Nilearn provides methods to define your own functional parcellation (using clustering algorithms such as k-means), and it also provides access to other atlases that have previously been defined by researchers.

Choosing regions of interest#

Nilearn ships with several atlases commonly used in the field, including the Schaefer atlas and the Harvard-Oxford atlas.

In this tutorial, we’ll use the MSDL (multi-subject dictionary learning; [VGP+11]) atlas, which defines a set of probabilistic ROIs across the brain.

msdl_atlas = datasets.fetch_atlas_msdl(data_dir=data_dir)

msdl_coords = msdl_atlas.region_coords
n_regions = len(msdl_coords)

print(f'MSDL has {n_regions} ROIs, part of the following networks :\n{np.unique(msdl_atlas.networks)}.')

Dataset created in ./nilearn_data/msdl_atlas

Downloading data from https://team.inria.fr/parietal/files/2015/01/MSDL_rois.zip ...

MSDL has 39 ROIs, part of the following networks :
['Ant IPS' 'Aud' 'Basal' 'Cereb' 'Cing-Ins' 'D Att' 'DMN' 'Dors PCC'
 'L V Att' 'Language' 'Motor' 'Occ post' 'R V Att' 'Salience' 'Striate'
 'Temporal' 'Vis Sec'].

 ...done. (1 seconds, 0 min)
Extracting data from ./nilearn_data/msdl_atlas/8eaecb9e05c478f565847000d9902a25/MSDL_rois.zip..... done.

It also provides us with easy ways to view these atlases directly. Because MSDL is a probabilistic atlas, we can view it using:

plotting.plot_prob_atlas(msdl_atlas.maps)

<nilearn.plotting.displays._slicers.OrthoSlicer at 0x7f2ee4df4d00>

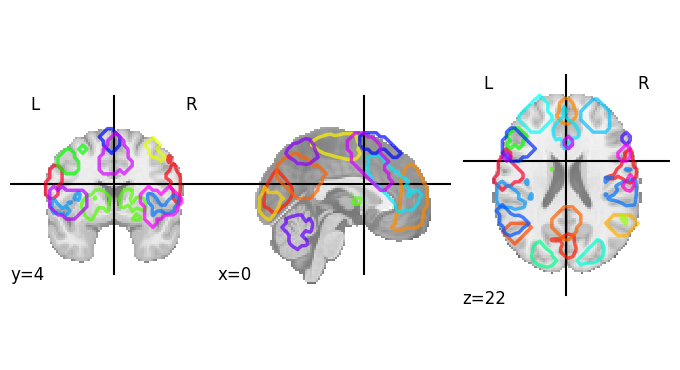
_images/826b0726a38a8f0107807f15cc2ab5233b2723e52058990c1e72c2edb05bb5c3.png

Different type of brain parcellation schemes

There are various ways of defining brain parcels. Largely we can classify them in two ways:

Functional vs anatomical
- Anatomical atlases use structural land marks to separate regions. Example: Harvard-Oxford atlas
- Functional atlases define regions based on the organisation of fMRI signal, such as functional connectivity. Example: Schaefer atlas
Probablility vs discrete segmentation
- Probabilistic segmentation: use contiunous, non-zero values to define parcels. Example: Difumo (functional), Hammersmith (anatomical)
- Discrete segmentation: parcels that have rigid boundaries. Example: BASC (functional)

It’s important to understand the method used for constructing the atlas of choice. For example, using a anatomical atlas to extract signal from functional data might not be the best thing. To find out more, watch this lecture from Brainhack School by Dr Pierre Bellec on brain parcellation in fMRI.

Applying a Masker object#

We’d like to supply these ROIs to a Masker object. All Masker objects share the same basic structure and functionality, but each is designed to work with a different kind of ROI.

The canonical nilearn.maskers.NiftiMasker works well if we want to apply a single mask to the data, like a single region of interest.

But what if we actually have several ROIs that we’d like to apply to the data all at once? If these ROIs are non-overlapping, as in discrete parcellations, then we can use nilearn.maskers.NiftiLabelsMasker. Because we’re working with probabilistic ROIs, we can instead supply these ROIs to nilearn.maskers.NiftiMapsMasker.

Mask your data!#

We can supply our MSDL atlas-defined ROIs to the NiftiMapsMasker object, along with resampling, filtering, and detrending parameters.

masker = maskers.NiftiMapsMasker(
    msdl_atlas.maps, resampling_target="data", detrend=True).fit()

One thing you might notice from the above code is that immediately after defining the masker object, we call the .fit method on it. This method may look familiar if you’ve previously worked with scikit-learn estimators!

You’ll note that we’re not supplying any data to this .fit method; that’s because we’re fitting the Masker to the provided ROIs, rather than to our data.

Dimensions, dimensions#

We can use this fitted masker to transform our data.

roi_time_series = masker.transform(development_dataset.func[0])
roi_time_series.shape

(168, 39)

If you remember, when we first looked at the data, its original dimensions were (50, 59, 50, 168). Now, it has a shape of (168, 39). What happened?!

Rather than providing information on every voxel within our original 3D grid, we’re now only considering those voxels that fall in our 39 regions of interest provided by the MSDL atlas and aggregating across voxels within those ROIS. This reduces each 3D volume from a dimensionality of (50, 59, 50) to just 39, for our 39 provided ROIs.

You’ll also see that the dimensions “flipped.” That is, we’ve transposed the matrix such that time is now the first rather than second dimension. This follows the scikit-learn convention that rows are samples and columns are features in a data matrix.

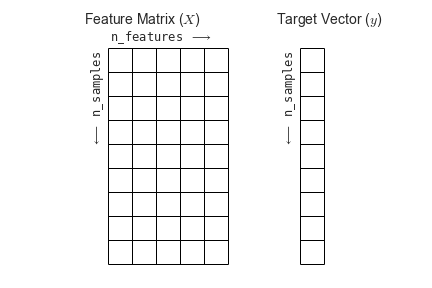
_images/samples-features.png — Fig. 4 The scikit-learn conventions for feature and target matrices. From Jake VanderPlas’s *Python Data Science Handbook*.#

One of the nice things about working with nilearn is that it will impose this convention for you, so you don’t accidentally flip your dimensions when using a scikit-learn model!

Creating and viewing a connectome#

Scientists have found that some cognitive functions involve the activity of neurons from an isolated region, and sometimes different regions of the brain interact together to perform a task. This functional integration leads to a description of the functional brain as a network. Formally, the co-activation of different time series is called functional connectivity.

The simplest and most commonly used kind of functional connectivity is pairwise correlation between ROIs.

We can estimate it using nilearn.connectome.ConnectivityMeasure.

from nilearn.connectome import ConnectivityMeasure

correlation_measure = ConnectivityMeasure(kind='correlation')
correlation_matrix = correlation_measure.fit_transform([roi_time_series])[0]

We can then plot this functional connectivity matrix:

np.fill_diagonal(correlation_matrix, 0)
plotting.plot_matrix(correlation_matrix, labels=msdl_atlas.labels,
                     vmax=0.8, vmin=-0.8, colorbar=True)

<matplotlib.image.AxesImage at 0x7f2ee4a12880>

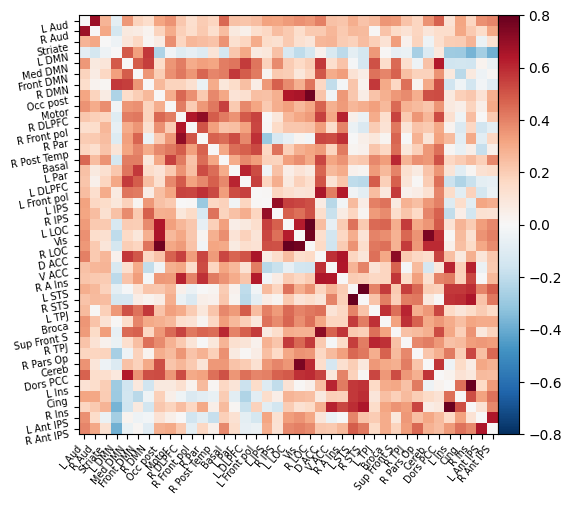
_images/5052462da28c0dcc0c0258aa36209135c154e58d80b019d945aa0933a4897745.png

Or view it as an embedded connectome:

plotting.view_connectome(correlation_matrix, edge_threshold=0.2,
                         node_coords=msdl_atlas.region_coords)

Accounting for noise sources#

As we’ve already seen, maskers also allow us to perform other useful operations beyond just masking our data. One important processing step is correcting for measured signals of no interest (e.g., head motion). Our development_dataset also includes several of these signals of no interest that were generated during fMRIPrep pre-processing. We can access these with the confounds attribute, using development_dataset.confounds.

Let’s quickly check what these look like for our first participant:

pd.read_table(development_dataset.confounds[0]).head()

	csf	white_matter	global_signal	std_dvars	dvars	framewise_displacement	t_comp_cor_00	t_comp_cor_01	t_comp_cor_02	t_comp_cor_03	...	cosine00	cosine01	cosine02	cosine03	trans_x	trans_y	trans_z	rot_x	rot_y	rot_z
0	439.699409	451.645460	525.387206	0.000000	0.000000	0.000000	-0.093142	-0.047009	0.110108	-0.132180	...	0.109104	0.109090	0.109066	0.109033	-0.000233	-0.076885	0.062321	0.000732	0.000352	0.000841
1	439.471640	451.103437	525.155030	0.940416	14.937284	0.055543	-0.091190	-0.075796	0.084680	-0.026517	...	0.109066	0.108937	0.108723	0.108423	-0.006187	-0.078395	0.056773	0.000112	0.000187	0.000775
2	439.744498	450.981505	525.324735	0.885710	14.068359	0.054112	-0.051778	-0.012647	-0.014665	0.003982	...	0.108990	0.108632	0.108038	0.107207	-0.000227	-0.069893	0.083102	0.000143	0.000364	0.000716
3	440.772620	450.600261	525.606646	0.864385	13.729636	0.057667	-0.025552	0.004938	-0.044833	0.077124	...	0.108875	0.108176	0.107012	0.105391	0.002492	-0.074707	0.060337	0.000202	0.000818	0.000681
4	440.115442	450.678959	525.656775	0.830847	13.196932	0.051438	-0.032434	-0.021743	0.003173	0.063508	...	0.108723	0.107567	0.105651	0.102986	-0.000226	-0.084204	0.085079	0.000183	0.000548	0.000682

5 rows × 28 columns

We can see that there are several different kinds of noise sources included! This is actually a subset of all possible fMRIPrep generated confounds that the Nilearn developers have pre-selected. For most analyses, this list of confounds is reasonable, so we’ll use these Nilearn provided defaults.

Never pass the full fMRIPrep confounds to the denoising function.

In the recent version of nilearn, we implemented function load_confounds and load_confounds_strategy to help you select confound variables based on existing literature and fMRIPrep documentations. User can select preset denoising strategies and the function will retrieve the relevant regressors. For more information, please refer to the this nilearn document.

Importantly, we can pass these confounds directly to our masker object:

corrected_roi_time_series = masker.transform(
    development_dataset.func[0], confounds=development_dataset.confounds[0])
corrected_correlation_matrix = correlation_measure.fit_transform(
    [corrected_roi_time_series])[0]
np.fill_diagonal(corrected_correlation_matrix, 0)
plotting.plot_matrix(corrected_correlation_matrix, labels=msdl_atlas.labels,
                     vmax=0.8, vmin=-0.8, colorbar=True)

<matplotlib.image.AxesImage at 0x7f2ee499ed30>

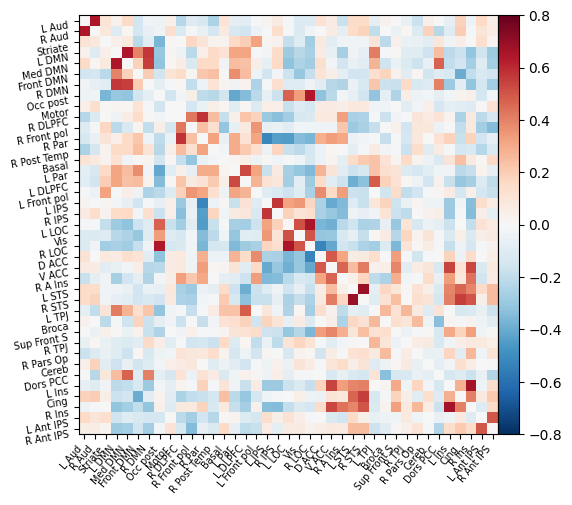
_images/7009aba381f69c44e37176680becc9f39a68515d3009032ee70fa9f62b539080.png

As before, we can also view this functional connectivity matrix as a connectome:

plotting.view_connectome(corrected_correlation_matrix, edge_threshold=0.2,
                         node_coords=msdl_atlas.region_coords)

In both the matrix and connectome forms, we can see a big difference when including the confounds! This is an important reminder to make sure that your data are cleaned of any possible sources of noise before running a machine learning analysis. Otherwise, you might be classifying participants on e.g. amount of head motion rather than a feature of interest!

Exercises!#

Load different atlases and view them!
- Try to load a different atlas availible through the nilearn.datasets module.
- Try to show one region of interest. You might need nilearn.images module.
Masker report!

Nilearn has added a new feature to generate visualised reports for the masker! Here is the relevant section. Try the report function on different type of maskers!
Try different options in plotting.plot_matrix
- In a new cell, try this command plotting.plot_matrix? to see the full documentation.
- See all these options we didn’t cover? Try them and see what changes in the figures.

References#

[Glo99]

G H Glover. Deconvolution of impulse response in event-related BOLD fMRI. Neuroimage, 9(4):416–429, April 1999.

[VGP+11]

Gael Varoquaux, Alexandre Gramfort, Fabian Pedregosa, Vincent Michel, and Bertrand Thirion. Multi-subject dictionary learning to segment an atlas of brain spontaneous activity. In Information Processing in Medical Imaging, 562–573. Springer Berlin Heidelberg, 2011.